Khi
sử dụng các dịch vụ do tổ chức IGS cung cấp hoàn toàn có thể đạt được độ chính
xác vị trí mặt bằng tương hỗ ở mức 1-3 mm và độ chính xác hiệu độ cao trắc địa
cao hơn 10 mm bằng công nghệ GPS [45].
Tuy
nhiên để đạt độ chính xác xác định vị trí của các điểm GPS ở mức một vài mm
không thể không tính đến sự ảnh hưởng của các yếu tố địa vật lý như ảnh hưởng của
tầng đối lưu, hiện tượng triều của vật thể Trái đất (Earth body Tide), sức tải
thuỷ triều đại dương (Ocean Tide Loading), thuỷ triều của cực Trái đất (Polar
Tides) và sức tải áp suất khí quyển
(Atmospheric Pressure Loading) [46].
Sự
biến dạng triều của Trái đất do sự hút của
mặt trăng và mặt trời có thể gây ra sự xê dịch vị trí mặt bằng và độ cao
ở mức 40 cm trong vòng 6h [51]. Thuỷ triều của đại dương gây ra sự
biến thiên có chu kỳ sức tải vật chất bề mặt trên mặt Trái đất và gây ra sự biến
dạng thuỷ triều ở mức 10 cm ở một số khu vực trên thế giới [52]. Hiện tượng triều
của cực Trái đất có thể gây ra sự xê dịch vị trí trên mặt Trái đất đến 15 mm
[53]. Sức tải áp suất khí quyển có thể gây ra sự xê dịch độ cao ở mức một vài mm
[54].
1. Nghiên
cứu ảnh hưởng của tầng đối lưu đến các trị đo GPS.
ảnh
hưởng của tầng đối lưu đến tín hiệu điện từ được chia thành 2 thành phần: thành
phần khô và thành phần ướt. ảnh hưởng của thành phần khô đến tín hiệu điện từ lớn
hơn ảnh hưởng của thành phần ướt. Thành phần khô được xác định dựa trên định luật khí lý tưởng đối với
không khí khô và chiếm khoảng 90% ảnh hưởng
của tầng đối lưu. Số cải chính vào giả cự ly do ảnh hưởng của thành phần khô của
tầng đối lưu đảm bảo để độ chính xác của
giả cự ly không tồi hơn 1cm [28]. Tuy ảnh hưởng của thành phần ướt có đại lượng
nhỏ hơn so với ảnh hưởng của thành phần khô, nhưng đại lượng này dao động mạnh
trong không gian và theo thời gian, thêm vào đó độ chính xác xác định đại lượng
này phụ thuộc vào độ chính xác của các
tham số khí tượng được xác định dọc theo đường truyền tín hiệu vệ tinh trong tầng đối lưu.
Đóng
góp của thành phần khô vào độ chính xác giả cự ly từ máy thu đến vệ tinh
được
đánh giá bởi đại lượng 0,3–5 m, còn đối với thành phần ướt 3–60 cm phụ thuộc
vào điều kiện khí tượng [28]. Do đó việc tính đến ảnh hưởng của tầng đối lưu đến
độ chính xác đo GPS là công việc bắt buộc.
Ảnh
hưởng của tầng đối lưu đến kết quả đo GPS là nhân tố cơ bản hạn chế độ chính
xác xác định hiệu độ cao trắc địa bằng công nghệ GPS [31]. Theo kết quả nghiên
cứu trong [29], với góc cao vệ tinh từ 15° trở lên, do ảnh hưởng của tầng đối lưu
sai số trung phương xác định hiệu độ cao trắc địa bằng công nghệ GPS được đánh
giá ở mức 3 lần lớn hơn sai số trung phương xác định cạnh đo. Trong [30]
còn chỉ rõ rằng sai số độ trễ tầng đối lưu
ảnh hưởng đến độ chính xác hiệu độ cao trắc địa ở mức 25mm đối với baseline dài
đến 50km.
Trong
công nghệ GPS, các số cải chính vào trị đo pha và giả cự ly do ảnh hưởng của tầng
đối lưu được xác định theo mô hình Seastamoinen hoặc mô hình modofied Hopfield
dựa trên việc xác định các tham số khí tượng (áp suất, nhiệt độ, độ ẩm) tại điểm
quan sát. Tuy nhiên các mô hình trên chỉ xác định số cải chính do ảnh hưởng của
các thành phần khô và ướt tại thiên đỉnh của điểm quan sát. Do đó các số cải
chính này còn được gọi là độ trễ
tầng đối lưu phương thiên đỉnh (Toposphere Zenith Delay - TZD). Để chuyển
các số cải chính nhận được về hướng từ máy thu đến vệ tinh, ở mức gần đúng xác
định, cần chia chúng cho SinE, ở đây E (Elevation) - góc nghiêng của tín hiệu vệ
tinh so với đường chân trời đi qua điểm quan sát.
Trong
trường hợp chung, số cải chính do ảnh hưởng của tầng đối lưu được xác định theo
công thức:
d = dd.md(E)
+ dw.mw(E),
ở
đây:
dd
- độ trễ tầng đối lưu phương thiên đỉnh
do không khí khô;
md(E)
- hàm ánh xạ (mapping function) của không khí khô;
dw.
- độ trễ tầng đối lưu phương thiên đỉnh do không khí ướt;
mw(E)
- hàm lánh xạ (mapping function) của không khí ướt;
E
- góc nghiêng của tín hiệu vệ tinh so với đường chân trời đi qua điểm quan sát.
Rất
nhiều nghiên cứu đã chỉ ra rằng việc tính độ trễ tầng đối lưu phương thiên đỉnh
theo các mô hình Seastamoinen hoặc mô hình modofied Hopfield dựa trên cơ sỏ xác
định các tham số khí tượng (áp suất, nhiệt
độ, độ ẩm) tại điểm quan sát không cho kết quả tốt hơn, và nhiều trường hợp cho
kết quả tồi hơn, so với việc sử dụng mô hình khí quyển chuẩn [30,32]. Ở Việt Nam
Việc
sử dụng mô hình khí quyển chuẩn không đòi hỏi phải xác định các tham số khí tượng
tại điểm đo GPS. Trong [57] giới thiệu mô hình khí quyển chuẩn được sử dụng
trong phần mềm Bernese. Dựa theo mô hình
này, áp suất P, nhiệt độ T theo thang độ Kenvin, độ ẩm tương đối e′ được xác định
theo các công thức sau:
ở
đây P0, T0, e0 - các giá trị được xác định
tương ứng với mực nước biển. Ví dụ P0 = 1013,25 mb, T0 =
291,2K; e0’=50 %; H - độ cao của trạm đo GPS.
Với
độ cao H đã biết của trạm đo GPS hoàn
toàn tính được các giá trị P, T,
e. Các giá trị này được đưa vào các công thức của mô hình Saastamoinen để tính độ trễ tầng đối lưu phương thiên đỉnh.
Độ trễ
tầng đối lưu
phương thiên đỉnh được
xác định theo mô
hình Saastamoinen và có dạng sau:
Đối
với thành phần khô:
ở
đây P- áp suất bề mặt Trái đất (mbar), F =1-0,0026.cosφ-0,0028.H,
φ- vĩ độ của điểm, H- độ cao trắc địa của điểm có đơn vị là
km.
Đối
với thành phần ướt:
T
- nhiệt độ không khí theo thang độ Kenvin, e - áp suất riêng của hơi nước
(mbar), Z – góc thiên đỉnh của tín hiệu
vệ tinh.
Để
chuyển độ ẩm tương đối e' sang áp suất riêng của hơi nước e sử dụng
công thức sau:
Trong
tài liệu [33], các tác giả đã khảo sát 15 hàm ánh xạ khác nhau được giới thiệu
khoảng 30 năm gần đây và kết luận rằng đa số các hàm ánh xạ đều cho kết quả tốt
với góc cao vệ tinh từ 15° trở lên. Tuy nhiên đối với những ứng dụng GPS độ
chính xác cao, các tác giả đề nghị nên
dùng các hàm ánh xạ của Lanyi, Herring, Ifadis hay Niell vì 4 hàm này vẫn cho kết
quả tốt với góc E hạ thấp đến 3°. Dạng đơn giản nhất của hàm ánh xạ được biểu
diễn như sau [ 115, p. 310 ]:
m(E)
= 1/sin(E).
Theo
[115], hàm ánh xạ m(E) có thể được tính theo mô hình Marini:
ở
đây ε=k/(1+k) ; k=B(φ,h)/d ; B(φ,h) - đại lượng biểu diễn hàm của độ cao h và
vĩ độ φ của trạm đo; δM - sự thay đổi tỷ lệ xích của số cải chính tầng đối lưu; d - độ
trễ tầng đối lưu phương thiên đỉnh của không khí khô hoặc không khí ướt.
Hàm
ánh xạ Niell do A.E. Niell giới thiệu gần đây nhất (1996) [34]. Nó thực ra bao
gồm hai hàm riêng biệt: một cho không
khí khô và một cho không khí ướt,
nhưng đều có dạng chung sau:
Trong
đó các hệ số a,b,c được xác định theo vĩ độ φ và thời điểm đo t. Đối với hàm ánh xạ khô, hệ số a tính như
sau (b và c tương tự)
Thời
điểm đo t được biểu diễn trong đơn vị ngày, T0 = 28. Các giá trị aavg, bavg, cavg,
aamp, bamp, và camp được xác định bằng cách nội
suy từ bảng dưới đây.
Hệ
số
|
Vĩ độ
|
||||
15°
|
30°
|
45°
|
60°
|
75°
|
|
aavg
bavg
cavg
aamp
bamp
camp
|
1.2769934e-3
2.9153695e-3
62.610505e-3
0.0
0.0
0.0
|
1.2683230e-3
2.9152299e-3
62.837393e-3
1.2709626e-5
2.1414979e-5
9.0128400e-5
|
1.2465397e-3
2.9288445e-3
63.721774e-3
2.6523662e-5
3.0160779e-5
4.3497037e-5
|
1.2196049e-3
2.9022565e-3
63.824265e-3
3.4000452e-5
7.2562722e-5
84.795348e-5
|
1.2045996e-3
2.9024912e-3
64.258455e-3
4.1202191e-5
11.723375e-5
170.37206e-5
|
Các hệ
số của hàm ánh xạ ướt được nội suy theo
bảng dưới đây.
Hệ số
|
Vĩ độ
|
||||
15°
|
30°
|
45°
|
60°
|
75°
|
|
a
b
c
|
5.8021897e-4
1.4275268e-3
4.3472961e-2
|
5.6794847e-4
1.5138625e-3
4.6729510e-2
|
5.8118019e-4
1.4572752e-3
4.3908931e-2
|
5.9727542e-4
1.5007428e-3
4.4626982e-2
|
6.1641693e-4
1.7599082e-3
5.4736038e-2
|
Như
vậy để tính các hàm ánh xạ Niell, chúng ta chỉ cần biết vĩ độ của trạm đo và thời
điểm đo mà không cần đến các tham số khí
tượng như nhiệt độ, áp suất và độ ẩm. Mặc dù tồn tại hai hàm ánh xạ riêng biệt
nhưng trên thực tế là chúng rất gần nhau. Vì vậy khi cần khảo sát chung độ trễ
thiên đỉnh của không khí ướt và khô, người ta thường sử dụng hàm ánh xạ ướt để
đại diện.
Mặt
khác cần lưu ý rằng độ trễ phương thiên đỉnh lại không phải là hằng số. Tham số
này biến động theo không gian và thời gian. Để xử lý tham số này, người ta có
thể giả sử rằng nó chỉ không đổi trong khoảng thời gian ngắn (1 - 2h) và sau
chu kỳ đó lại thêm vào mô hình một tham số mới. Cách xử lý thường được chọn là
nhảy bậc (step wise) và bước ngẫu nhiên (random walk process).
Do sự gần đúng của các mô hình tính số cải chính
do ảnh hưởng của tầng đối lưu, nên trong quá trình xử lý dữ liệu GPS còn cần đưa
số cải chính tính đến sự gần đúng của các mô hình nêu trên dưới dạng ẩn phụ
trong phương trình các trị đo GPS. Trong trường hợp này, việc khảo sát ảnh hưởng
của góc E đến độ chính xác của hiệu độ cao trắc địa được trình bày trong [37].
Vấn đề này cũng được nghiên cứu trong nhiều tài liệu, ví dụ [35, 36, 37, 108].
Các kết quả nghiên cứu trong [37] cho thấy rằng khi góc ngưỡng vệ tinh ở mức 50,
độ chính xác của hiệu độ cao trắc địa được nâng lên đáng kể và tương đương với
sai số vị trí tương hỗ mặt bằng. Việc
xác định số cải chính do ảnh hưởng của tầng đối lưu vào các trị đo GPS theo mô
hình cần được tiến hành sau mỗi 2 - 6h [38]. Dưới góc E thấp ảnh hưởng của hiện
tượng đa đường truyền sẽ mạnh lên. Để khắc phục điều này sử dụng các dạng ăng
ten chuyên dụng, ví dụ ăng ten vòng cảm kháng cao tần đường kính 85 cm (85 diameter choke ring) [39].Bài tiếp theo: Ảnh hưởng của các yếu tố địa vật lý đến chất lượng đo GPS với khoảng cách lớn-Phần 2
Hãy like nếu bài viết có ích →
Kết bạn với gisgpsrs trên Facebook
để nhận bài viết mới nóng hổi







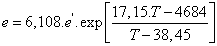



Không có nhận xét nào:
Đăng nhận xét