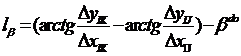Trắc địa là một nghành khoa học
chuyên nghiên cứu về hình dạng, kích thước quả đất, về các phương pháp đo đạc
và biểu thị bề mặt quả đất dưới dạng bản đồ và số liệu. Khi ta xử lý các số liệu
đo nếu bằng sức người thì mất rất nhiều thời gian và độ chính xác không được
cao. Với sự hỗ trợ của công nghệ thông tin thì ta không còn bận tâm điều đó nữa.
Việc tính toán đó được lập trình thành các chương trình và chúng xử lý. Hiện tại
có rất nhiều ngôn ngữ lập trình như: Pascal, C, C++,VC++, VB, C#…thì chúng ta
có thể dễ dàng lập trình những chương trình cơ bản trong trắc địa để tiện khi
tính toán.
Trong bài này sẽ hướng dẫn sử dụng
ngôn ngữ C để viết chương trình bình sai gián tiếp lưới mặt bằng. Quá trình lập
trình gồm các bước: Quy trình, thuật toán bình sai theo phương pháp gián tiếp.
Tổ chức cơ sở dữ liệu. Lập các modul chương trình. Ta đọc dữ liệu đầu vào từ một
file và sau khi xử lý bình sai sẽ xuất ra một file để cho người tiến hành bình
sai lấy kết quả một cách dễ dàng.
I. Cơ sở lý thuyết
Ta có n giá trị thực của dãy
trị đo: y1, y2…yn có thể được biểu diễn dưới dạng
hàm số của các ẩn số x1, x2…xk
Trị gần đúng được ký hiệu: y1(0); y2(0);
…; yn(0); x1(0); x2(0);
… ; xk(0);
Trị sau bình sai sẽ được xác định là:
Chúng
ta sẽ có phương trình liên hệ như sau:
Trị gần đúng của các giá trị đo y1(0)
được chọn bằng giá trị đo. Thực hiện khai triển theo công thức Taylo:
Các chỉ số (0) ký hiệu các đạo hàm riêng được tính
theo các giá trị gần đúng. Đối với các hàm tuyến tính các giá trị của đạo hàm
riêng không phụ thuộc vào các giá trị gần đúng. Phương trình (1.2) có thể được viết lại:
Phương trình (1.3) được gọi là phương trình các số
hiệu chỉnh . Số các phương trình này bằng số các trị đo n.
Theo nguyên tắc số bình phương trình nhỏ nhất phải
tìm lời giải thoả mãn điều kiện [pvv]=min Hệ phương trình các số hiệu chỉnh có dạng sau:
Biểu
diễn hệ phương trình (1.4) dưới dạng ma trận:
A∆x +L =V.
Ở đây ma trận:
Như chúng ta đã biết [pvv] =min, cần có biểu
thức sau:
Từ tính chất
(ABC)T =CTBT.AT
Suy ra:
AT.P.V =0 (1.6)
Biểu thức (1.6) được gọi là bổ đề GAUSS.
Từ (1.6) ta có phương trình sau:
AT.P(A.∆x +L) =0
AT.P.A.x +ATPL
=0
R.∆x +b =0 (1.7)
Ở đây
R =AT.P.A
b =AT.P.L
Hệ phương trình (1.7) được gọi là hệ phương trình
chuẩn
Các ma trận hệ số R và b được xác định như sau
II. Quy trình, Thuật toán bình sai theo phương pháp gián tiếp.
1) Chọn ẩn số.
Ø
Xác
định tọa độ gần đúng: X(0). (Tùy vào mỗi lưới thì ta tính X(0)
khác nhau.)
Ø
Ẩn
số là vectơ số gia tọa độ của các điểm mới.
δX = (dx1, dy1, dx2,
dy2, ..., dxk, dyk)T
2) Lập phương trình số hiệu chỉnh.
A.δX + L = V
a1.dx1 + a2.dy1
+ a3.dx2 + ... + a2K+1.dxK + a2KdyK
– a2K+1 = V
a) Phương trình số hiệu chỉnh của
phương vị đo.
Với trị đo góc phương vị ta viết được đẳng thức:
α’KJ = αKJ + vα
= αoKJ + dαKJ
Hay
Vα = dαKJ + (αoKJ
– αKJ) = dαKJ + lα
Vα = aKJdyK + bKJ.dxK - aKJ.dyJ – bKJ.dxJ
+ lα
b) Phương trình số hiệu chỉnh của góc
đo.
β = αIK + αIJ
vβ = vαIJ – αIK
vβ = (aIK - aIJ)δXI + (bIK –
bIJ)δyI – aIKδXK – bIKδyK
+ aIJδXJ + bIJδyJ + (lαIK
– lαIJ)
Sai số trị
đo góc: Các góc có sai số bằng nhau mβ
c) Phương trình số hiệu chỉnh của cạnh.
VS
= - cosαIJδXI – sinαIJδYI + cosαIJδXJ
–sinαIJδYJ + lS
lS
= S - Sdo
Sai số trị
đo cạnh: mS = (a + b.D.10-6) (mm)
3)
Lập
hệ phương trình chuẩn
AT.P.A.δX
– AT.P.L =0
R.δX –
b = 0
4)
Giải
hệ phương trình chuẩn
δX = - R-1.b
Ø Phương pháp khử: - Gauss
- Khai căn.
Ø Theo phương pháp khai căn: RδX + b = 0
TT.T.δX + b = 0
(T: là ma trận chéo dưới)
T.δX + (TT)-1.b
=0
T.δx + b’ = 0
Ø Tính nghiệm :
§
Tính
từ dưới lên :
§ Tính lại tọa độ gần đúng.
Xi = X(0)i
+ δXi
Lặp lại từ bước 2
đến bước 4. Kết thúc lặp khi tọa độ cuối cùng đạt một độ chính xác nào đó thì
thôi lặp.
5)
Đánh
giá độ chính xác
Ø Tính
Ø Tính sai số cạnh yếu trong lưới
Sai số chiều dài
cạnh
Sai số phương vị
cạnh
Sai số tương hỗ vị
trí điểm
Hãy like nếu bài viết có ích →
Kết bạn với gisgpsrs trên Facebook
để nhận bài viết mới nóng hổi